【事例】マーケティング効果検証のデータサイエンス実務から見えた課題と解決策～アポロでの具体的な取り組み〜

Introduction

前回の記事では、効果検証の際にはバイアスをいかに取り除き、反実仮想※を作るために並行トレンドを担保する必要があるという話をした。今回は実際に、アポロ社内でどのように効果検証を行なっているかを、取り組みとともに紹介する。
※事実と反対のことを想定すること

効果検証の実際の事例

効果検証の際には2つのグループを用意する。施策によって介入がされた『介入群 (test group)』 と呼ばれるグループと、介入がされなかった『比較対象群(control group)』のグループだ。その差分を取って効果量の推定をすることが、一般的な効果検証になる。
この時に「比較対象群」は、介入群と同じようなグループで、かつ施策の影響を受けていないことが必要になる。

すなわち

1. 比較対象群からバイアスをいかに取り除くか
2. 介入群と比較対象群とで、並行トレンドをいかに担保するか

が重要になる。

しかし実務では、
事例1: 事前に介入群と比較対象を選べる場合
事例2: 比較対象群を持っているデータの中からリーズナブルに選定する場合
事例3: そもそも比較対象群を事前に用意できない場合
がある。
アポロでは、それぞれについてのノウハウを溜めており、その知識や技術、経験の蓄積を基に分析を行っている。

事例1: 事前に介入群と比較対象を選べる場合

介入群と比較対象を選ぶ際には、常にセレクションバイアスに気を付けなければならない。しかし、よく使われる手法として、ランダム化比較試験(RCT randomized controlled trial) がある。RCTでは、事前に介入群と比較対象群を同じ母集団からランダムに選定する手法で、バイアスを最小限にする目的でよく用いられる。

例えば、クーポンを配る例で考えてみる。この時、会員のみにクーポンを配ったとして正しく効果検証する際にはどうしたらよいか? RCTを使うのであれば、全会員のうち、クーポンを配る人、配らない人をランダムに選択することで、バイアスを抑えた効果検証が可能である。この時、20代男性 に偏りすぎる、といったことがないようにできる限り人数は多く、かつ母集団の中で属性の偏りがないことが理想だ。

こうすることで、同じような人たちの集まりから、同じように選んできていることがある程度保証できるため、効果検証として信頼性が高いものになる。

事例2: 比較対象群を適切に選択した効果検証

実際のケースを紹介しながら説明してみる。 比較対象群を設定する際には、事前に設定する場合と、事後に設定する場合のどちらもがある。そのどちらにおいても、粒度が細かくなりすぎて、並行トレンドを担保できないことが多くある。

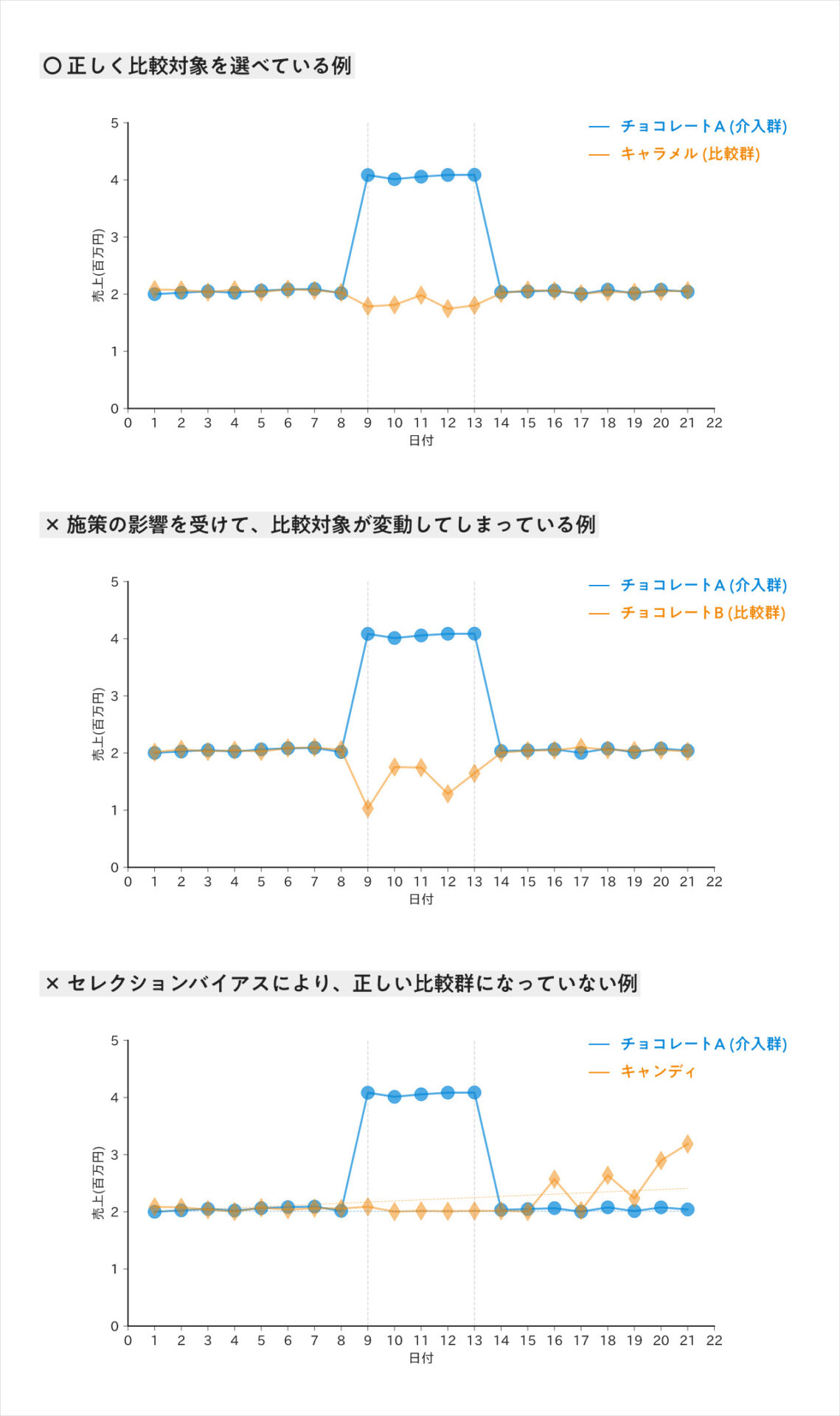
例えば、小売業界でチョコレートという商品だけにクーポンを配り、その効果検証をする際には、どのような比較対象群を取れば良いのか？

理想を言えば、クーポン対象、クーポン対象外といったように、条件の異なるチョコレートを比較すれば良いのかもしれない。 しかし前回の記事で紹介したように、比較対象群がクーポンの影響を受けてしまうため、正しい効果検証には至らない。また違う商品を比較対象に選んでいる以上、セレクションバイアスも生まれてしまう。

真に正しい効果検証を行うためには、何を比較対象に取れば良いのか。
ここがデータサイエンティストの腕の見せ所だ。

比較対象群のリーズナブルな選定

比較対象群の条件として

1. バイアスを極力小さくすること

2. 施策前後での振る舞いが変わらないこと=特定のトレンドを持たずに、並行トレンドを担保すること

の2つが必要だ。
先の例で言えば、チョコレートに似た売り上げのトレンドを持ち、かつクーポンの対象をチョコレートのみにした場合でも影響を受けない商品を、比較対象として選ぶことで解決できる。

チョコレートに似た売り上げは、どのように判断するのか。
例えば熟練のマーケターが、チョコレートと似たキャラメルを選ぶべきだと判断してもらうといった話でも良いが、それもまた主観によるバイアスが入っていて適切ではない。

そこで、数学的な手法を用いて、他のカテゴリの売り上げ推移を集計、チョコレートのクーポンを配る前と同じような振る舞いをしているカテゴリを選定する方法がある。
動的時間伸縮法(Dynamic Time Warping)と呼ばれる手法だ。これは時系列データを比較し、類似度を数字として出すことができる。時系列を基準にして類似したデータを読み解くと、2通りの考え方が見えてきて、波形が瞬間で等しいという考え方と、形は同じだが実はその時期がずれているだけといった考え方がある。その両方を加味し、総合的に似た時系列を数字で判断ができる手法がDTWだ。

このDTWで比較対象群を選定すれば、少なくとも施策実施前の並行トレンドは担保できる。つまりチョコレートとキャンディは、クーポンを配る前では売上が似ていて、定量評価によってキャンディを比較対象として選ぶことができる。

しかしキャンディは、チョコレートに対してクーポンを配った後に、チョコレートと同じクーポンが無い状態での反実仮想を再現できるのだろうか？

施策実行前の並行トレンドが担保されていたとしても、施策実行後の並行トレンドが保証されるわけではない。キャンデイを選んだことによりバイアスが乗るため、必ずしも比較対象として正しいと言い切ることはできない。
そのため、DTWで最適といわれたカテゴリのなかでも、さらにセレクションバイアスを除く工夫が重要になる。

比較対象群のセレクションバイアスを取り除く

セレクションバイアスを除くためにどんな方法が用いられるのか。

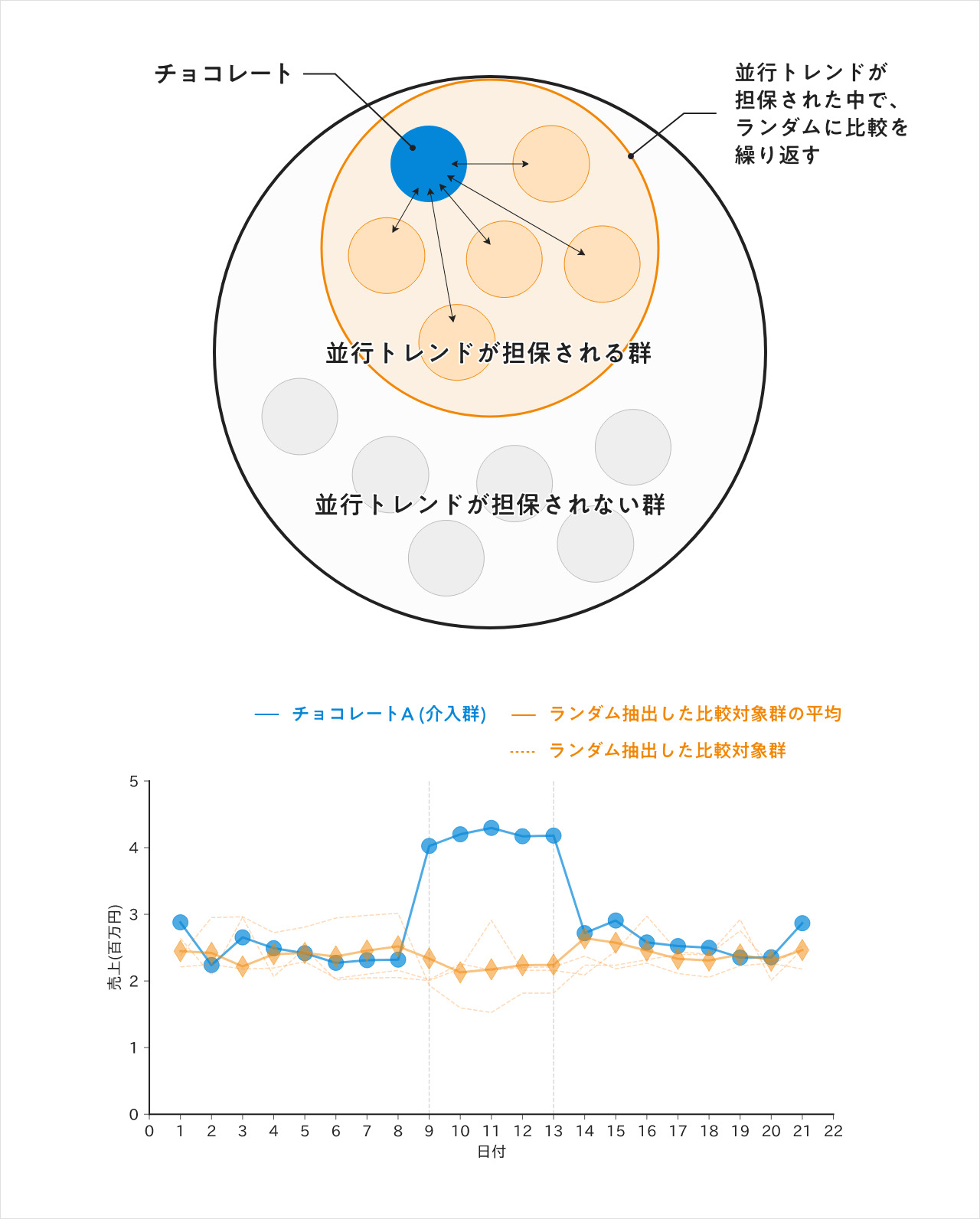
それはRCTのアナロジーでバイアスを減らすことができる。DTWで一度並行トレンドがある程度担保されるカテゴリを選定し、その中からいくつかをピックアップし組み合わせた『比較対象群A』、そしてまた同様にいくつかをピックアップした『比較対象群B』の複数の比較対象を用意する。

こうした比較対象群の選定を何回か繰り返すと、統計学でいう中心極限定理のようなことが起きます。それによりチョコレートとキャンディの単純比較よりも、バイアスを取り除くことができる。

このように、比較対象をいくつも作り、検証を行うこと(もしくは効果検証の文脈だけでなく、様々なサンプリングを用意して検証をすること)は、『交差検証 (cross validation)』とよばれ、より頑健で、信頼性の増した結果を得ることができる。

今回のチョコレートの例では

1. DTWで チョコレートに似たカテゴリ、キャンディ、チューイングガム、せんべい、タブレット、エナジードリンク、栄養ドリンクなどのカテゴリをいくつか選定
2. 比較対象群をA(キャンディ, チューイングガム)、B(チューイングガム、栄養ドリンク)、C(せんべい、タブレット)、D(キャンディ、せんべい)のように数パターンを用意し、チョコレートと比較

することで、効果検証が可能だ。

事例3: 比較対象がない場合の効果検証

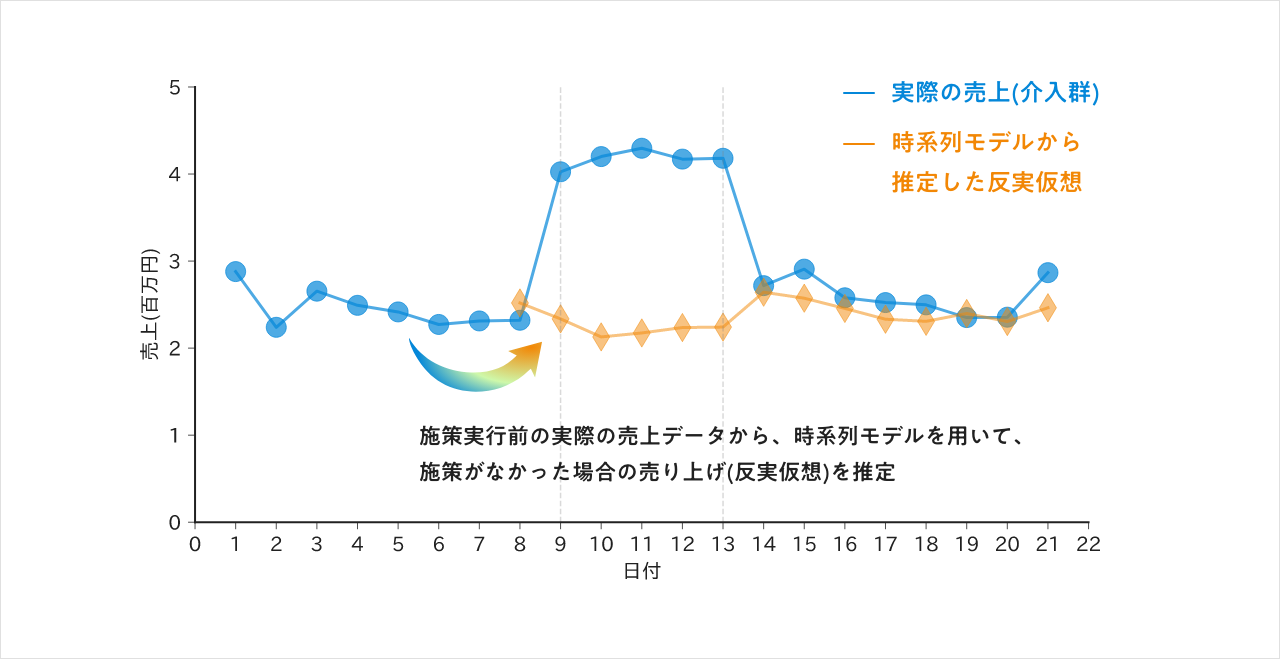
一方で、比較対象が作れない場合もある。チョコレートの例でいえば、チョコレート専門店で、商品単体では無く、その店全体でディスカウントをするような場合だ。この場合、比較対象をディスカウントをしなかった場合の店全体の売上を、反実仮想としておき比較する必要がある。

この反実仮想はどのように作るのかというと、ディスカウントをする前の値を使い、売り上げ予測のようなことができれば、比較することが可能である。また便利なツールとして、Facebookが提供する『Prophet』と呼ばれる時系列予測のパッケージがある。

Prophet では、売り上げを関数としてフィッティングをし、実際の売上 = (長期的なトレンド) + (周期性) + (特定のイベント成分) + (ノイズ) と要素を分け、学習予測をする。つまり、実際の売上をディスカウント前後で集計してProphet で学習させ、その結果からイベント成分を除くことで、反実仮想を作るという考えだ。

時系列の予測では、ARIMA(Auto Regressive Integrated Mean Average)モデルのような、ノイズや過去の実績から次を予測することができる古典的なモデルもある。ですがそれでは今回の例のような、イベント成分だけを除いた検証は難しい。また状態空間モデルで見るような、ある時点の売り上げは、その瞬間での他の売り上げや天気、店にいる人の数といったモデルで推定することも可能だが、その一方で状態空間モデルでは組み込む変数の量が多く、今回のようなスピーディーに効果検証をしたい場合では、労力がかかりすぎてしまうという欠点がある。

その点Prophetは、簡単な設定のみでイベント成分だけを除いた結果をある程度推定することができ、大変優れている。

このように、例え比較対象がない場合でも、手法を工夫することによって検証ができる場合もある。

最後に

単に効果検証と言っても考慮するべき点は多く、単純比較のみでは正しい検証はできない。今回は、事例による説明と、アポロではその課題をどのように解決しているかを紹介した。
このような検証もすぐにできたわけではなく、数々の試行錯誤の中で生まれたものである。その時々によって最適な手法は、これからも変わっていく。

こういった効果検証をすることが事前にわかっているのであれば、そもそもの施策の設計を検証可能な形に提案することもデータサイエンティストの役割である。毎度同じような検証方法では誤った結論を導いてしまうため、正しく検証できる方法を常に検討するのもデータサイエンティストの役割だ。